温故：线性表|数据结构

对 数据结构 - 线性表 进行温故，以期获新知

温故系列是我尝试的一种新学习总结方式，在 阅历增长时，总结旧闻，以 期获 新知，并不断迭代。了解更多

本次温故时间：2021年3月

注：部分图片来自网络检索，未找到出处，内容仅供学习，如有侵权，可留言联系 要求删除 或者 要求指明出处

基本概念

线性表 ，全名为 线性存储结构，是一种 有序数据项 的 集合，其中每个数据项都有 唯一 的 前驱 和 后继， 注意：第一个没有前驱，最后一个没有后继。

新数据项加入到数据集中时，只会加入到原有某个数据项 之前 或者 之后

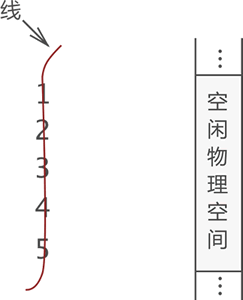
从上图我们可以理解，线性表是将数据项串起来 之后 存入物理空间 的一种数据结构。

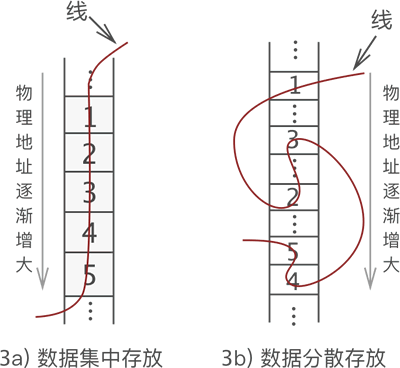
不同的存储方式，衍生出两种实现方式：

• 将数据 依次存储 在 连续的整块 物理空间中，是 顺序存储结构 又称 顺序表；
• 将数据 分散存储 在物理空间中，并能够存储数据项之间的 前、后驱 关系，是 链式存储结构 ，又称 链表；

顺序表

其性质可以直接对应到 数组，具有随机读写能力，使用需要先初始化，获取 整块的存储空间，如果使用中需要扩容， 则需要先分配一块新的存储空间，并进行内容复制。

链表

普通链表又称单链表，用于存储逻辑关系为 "一对一" 的数据。

与顺序表不同，链表不限制数据的物理存储状态，即数据项的物理存储位置是随机的。

每个 节点 对应一个数据项，包含了两部分信息：

• 数据元素本身，其所在的区域称为 数据域；
• 指向 直接后继元素 的指针，所在的区域称为 指针域；

头指针 ：一个普通的指针，它的特点是永远指向链表第一个节点的位置。

头节点 ：一个 不存任何数据 的空节点。不是必须的，但可以解决一些实际问题：

• 链表数据变动时，需要维护 链表的引用地址 即 头指针 的问题
• 遍历时，不需要对第一个节点进行特殊处理

首元节点 ：链表中第一个存有数据的节点为首元节点。

静态链表

比较早期的时候，并不能像C语言那样灵活的操作指针，于是用 数组代替指针 来描述单链表。 这种用数组描述的链表叫做静态链表，这种描述方法叫做 游标实现法。

算法题小练手

206.反转链表

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

进阶: 你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

来源：力扣（LeetCode）

迭代思路：遍历整个链表，将每个节点的next指向前驱，返回链表的尾端节点即可。

public ListNode reverseList(ListNode head) {
    ListNode prev = null;
    ListNode curr = head;
    ListNode tmp = null;
    while (curr != null) {
        tmp = curr.next;
        curr.next = prev;
        prev = curr;
        curr = tmp;
    }
    return prev;
}

递归思路： 递： 将结点的 后继 作为 新的链表头节点，调用reverseList，直到进行到原始链表的尾端时，即 node.next 为 null 时。此时开始归，返回新链表头节点

归：归的过程中，反转链表的方向，设原先有 a.next = b, 现在需要转变为 b.next = a, 即 a.next.next = a,

边界问题：

• 因为是在归中处理，所以相当于是从 原链表尾端 开始处理反转，开始位置不用担心
• 结束位置需要注意，必须将其的 next 改为 null，即 a.next = null

我们再用数学归纳法复盘一下：令长度为l （L的小写，部分字体下看起来像数字1，特此说明），原链表头结点为head

• 当l=0时，直接返回null，head也是null
• 当l=1时，直接返回head
• 当l=2时：
  • 取head的next，作为新链表先进入处理，返回结果即newHead，新链表长度l=1，直接返回了,确实是期望的反转链表的头节点
  • 反转两者(即 head 与 head.next)前后驱关系，head.next.next = head，处理head的next 为 null
  • 返回newHead
• 当l=3时：
  • 取head的next，作为新链表先进入处理，返回的newHead 是期望的 反转链表的头结点
  • 处理head 与 head.next 的前后驱关系，head.next.next = head，处理head的next 为 null
  • 返回newHead

......

• 当l=n，n>3时：
  • 取head的next，作为新链表先进入处理，返回的newHead 是期望的 反转链表的头结点
  • 处理head 与 head.next 的前后驱关系，head.next.next = head，处理head的next 为 null
  • 返回newHead
• 当l=n+1,n>3时：
  • 取head的next，作为新链表先进入处理，返回的newHead 是期望的 反转链表的头结点
  • 处理head 与 head.next 的前后驱关系，head.next.next = head，处理head的next 为 null
  • 返回newHead

我们依据数学归纳法，得出：l=0或l=1时，返回head，l >= 2时，处理方式一致，不再誊写

public ListNode reverseList(ListNode head) {
    //l=0时，head为null；l=1时，head.next 为null。 均直接返回head，归的特殊处理
    if (head == null || head.next == null) {
        return head;
    }
    //递
    ListNode newHead = reverseList(head.next);

    //归的处理
    //反转 head 与 head.next 的前后驱关系
    head.next.next = head;
    head.next = null;

    //返回newHead
    return newHead;
}

温故总结

作为比较基础的内容，在更复杂的数据结构中，线性表可能会作为底层实现。在实际应用中，我们用到 单链表 的地方不会太多。

在算法练手环节中，突然发现一个 很趁手 的东西，以为考虑 递归实现 思路时，我总是要非常仔细的思考边界问题。

但这次突然发现，若能够 被递归实现，一定可以用 数学归纳法 论证 做法的正确性，推导过程可以 完善地 讨论边界问题。 并且其推导过程非常 人性化。

这篇内容很短，就到此结束了。